Mécanismes cérébraux sous-tendant les inférences sur les intentions d’autrui lors de décisions collectives
Bien que la prise de décision dans un contexte social soit omniprésente et centrale dans nos sociétés, les algorithmes développés par le cerveau pour régir nos interactions sociales restent mal compris. En particulier, le fait que nos décisions sociales reposent sur l’attribution d’intentions à autrui a été jusqu’à présent sous-estimé. Des chercheurs, en collaboration avec une équipe américaine de l’Université de Washington (Seattle), montrent qu’un modèle probabiliste dépasse les modèles existants pour prédire quantitativement le comportement humain lors d’interactions de groupe. Ces résultats suggèrent que dans une tâche de prise de décision impliquant des membres anonymes, notre cerveau utilise des inférences bayésiennes pour modéliser l’esprit coopératif du groupe, en faisant des prédictions sur les décisions des autres simulant également les effets de leurs propres actions sur la dynamique du groupe. Ce travail est publié dans la revue Science Advances.
Pour prendre des décisions dans un contexte social, les hommes doivent prédire le comportement des autres et se représenter leurs intentions, une capacité connue sous le nom de "théorie de l'esprit". Un tel modèle des intentions des autres devient particulièrement complexe lorsque le nombre de personnes avec lesquelles on interagit simultanément est grand et que les actions sont anonymes. Ainsi, lorsque nos décisions sont réalisées dans un contexte social, le degré d’incertitude sur les résultats possibles augmente drastiquement. En effet, les comportements des autres individus sont bien plus difficiles à prédire que les changements physiques de notre environnement. Comparés aux objets inanimés, les comportements observables des autres ne fournissent que des informations partielles sur leur comportement futur. Ceci rend extrêmement difficile d’étudier la nature des algorithmes qui peuvent rendre compte de la prise de décision sociale.
Comment alors caractériser les principes computationnels sous-jacents à la prise de décision sociale ? L’hypothèse principale de ce travail est que lorsque nous sommes dans un contexte social interactif, notre cerveau effectue des inférences bayésiennes par lesquelles il calcule les probabilités que l’autre possède telle ou telle intention à partir d’observations. Ici les participants réalisaient une expérience comportementale connue sous le nom du dilemme du volontaire. Celui-ci illustre une situation où chacun de N joueurs a le choix de faire ou non un petit sacrifice pour le bien commun, dont tous bénéficieront, ou alors de ne pas participer à ce bien commun (‘Free Rider’). Dans une telle situation, les individus préfèrent que quelqu’un d’autre qu’eux-mêmes soit volontaire pour faire quelque chose, mais préfèrent quand même être volontaire dans le cas où ils sont sûrs qu’un nombre insuffisant de personne ne le soit pour générer le bien public.
29 participants ont réalisé 14 sessions contenant chacune 15 tours avec un même groupe de 4 autres joueurs (N=5). A chaque nouvelle session, les participants jouaient avec un autre groupe de joueurs. Au début de chaque tour, chaque joueur recevait E=1 unité monétaire (UM), et devait choisir entre 2 options : contribuer au bien public ou garder l’unité monétaire pour lui-même. La contribution avait un coût C de 1 UM. Le bien commun était produit comme une récompense pour l’ensemble du groupe (Gain=G= 2 UM pour chaque joueur) si et seulement si au moins k joueurs contribuaient chacun 1 UM. k valait 2 ou 4 selon la session. Après chaque tours le nombre de contribution, d’absence de contribution et le résultat global était révélé (succès ou échec à sécuriser les 2 ou 4 UM pour la récompense de groupe). Cependant, les joueurs étant anonymes, chaque action individuelle restait inconnue des autres joueurs. Les participants croyaient réellement interagir avec d’autres personnes mais ils jouaient en réalité avec un ordinateur qui générait les actions des 4 autres personnes. Personne n’était informé de l’identité des autres personnes avec lesquelles il interagissait. Le montant résultant après un tour était calculé comme ceci: E - C + G = 2 UM pour un participant ayant contribué et E+ G = 3 UM pour un participant n’ayant pas contribué au bien public (‘free-rider’) lorsque ce bien public était produit (le round était un succès). Si aucun bien commun n’était produit (le tour était un échec), le contributeur recevait E - C = 0 UM et celui n’ayant pas contribué recevait E = 1 UM.
Pour modéliser la façon dont nous prédisons les intentions d’autrui, les chercheurs ont utilisé des approches mathématiques dans lesquelles l’effet des actions d’un agent est incertain et dans lesquelles l'agent n'a qu'une information partielle de l'état courant. La nature novatrice de cette étude est d’établir une base théorique permettant de décrire les mécanismes neuro-computationnels sous-jacents aux décisions sociales (i.e. des algorithmes de calcul potentiellement adoptés par le cerveau pour inférer les intentions d’autrui).
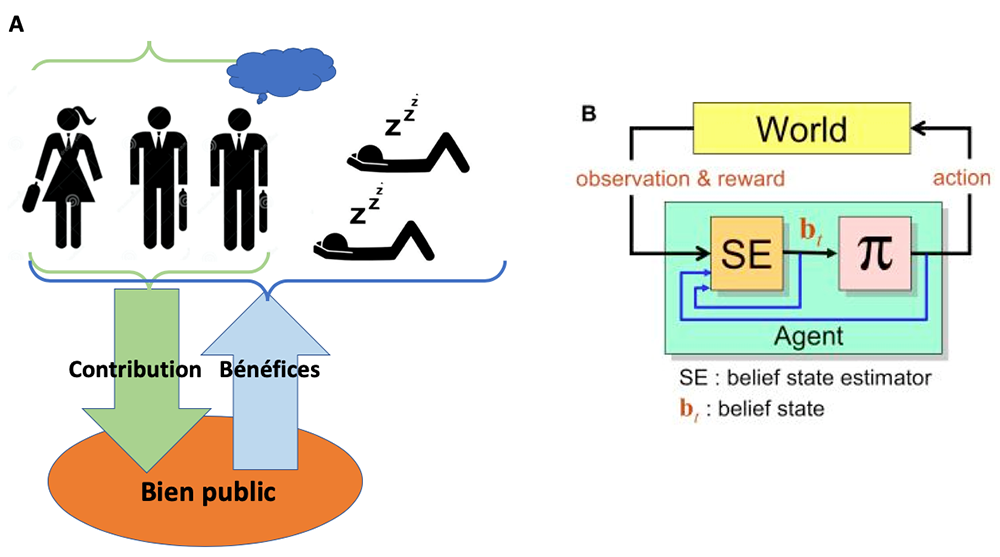
Figure : Le jeu de bien public (à gauche) et le modèle POMDP (à droite). Modèle POMDP du jeu de bien public. Modèle: Le participant infère la probabilité moyenne de la contribution du groupe mais ne la connaît pas explicitement. Le modèle suppose que le sujet maintient une croyance (notée bt) sur cette probabilité et la met à jour après avoir observé le résultat des contributions (ct) des autres à chaque tour. Sélection des actions : le modèle POMDP choisit une action (at) qui maximise la récompense totale attendue sur l’ensemble des prochains tours. Cette attente est basée sur sa croyance en cours et les conséquences de son action (contribution ”c” ou non contribution) sur le comportement du groupe dans les tours à venir.
Pour en savoir plus :
Modeling other minds : Bayesian inference explains human choices in group decision-making
Khalvati K, Park SA, Mirbagheri S, Philippe R, Sestito M, Dreher JC, and Rao RPN
Science Advances, 27 November 2019. doi: 10.1126/sciadv.aax8783