Existe-t-il des mélodies naturelles ?

Dans presque toutes les cultures humaines, la musique repose sur des échelles de la hauteur tonale.  Ces échelles définissent, pour créer mélodies et harmonies, un petit nombre de rapports de fréquence admissibles entre deux notes, parmi une infinité de possibilités. Beaucoup d'échelles utilisent les rapports simples 2:1, 3:2 et 4:3, correspondant à des intervalles appelés "octave", "quinte" et "quarte" dans la musique occidentale.

Pourquoi ces rapports sont-ils si courants ?

La présence de rapports simples dans les échelles musicales est généralement expliquée par le fait qu'ils favorisent la consonance de notes simultanées, en raison de phénomènes physiques et sensoriels. Pour des notes successives, par contre, l'opinion dominante est qu'il n'y a pas d'intervalle plus « naturel » qu'un autre. Certes, une mélodie reposant sur une échelle incluant l’octave, la quinte et la quarte sera souvent perçue par un auditeur occidental comme « plus harmonieuse » qu’une autre. Mais cette préférence est souvent attribuée à un phénomène d’acculturation, où l’on tend à préférer ce qui nous est familier et nous sommes tous, musiciens ou non, habitués aux échelles comportant des rapports simples.

L'étude publiée dans Current Biology suggère que, contrairement à l'opinion dominante, l'octave, la quinte et la quarte sont bien des intervalles mélodiques naturels, rendus perceptivement spéciaux par le fonctionnement du système auditif de tout être humain, quelle que soit sa culture.

La démonstration des scientifiques a consisté à entraîner des jeunes adultes occidentaux à détecter des anomalies ("fausses notes") dans des mélodies aléatoires de sons purs, basées sur diverses échelles musicales. Certaines de ces échelles ont été spécialement conçues pour cette étude. L’expérience ne nécessitait aucune connaissance musicale préalable. L'entraînement était long, de façon à aboutir à une saturation de la familiarité avec les échelles. Le principal résultat montre que les sujets ont mieux réussi avec les échelles comprenant des rapports fréquentiels simples. (2:1, 3:2, et 4:3), non seulement au début de l'entraînement – ce qui pourrait a priori être interprété comme un effet de familiarité (acculturation) – mais aussi à la fin de l'entraînement, qui avait compensé le désavantage éventuel d'un manque initial de familiarité. Un modèle computationnel suggère que ces rapports simples sont mieux représentés en mémoire, ce qui pourrait expliquer les résultats comportementaux.

L’étude suggère donc que l’usage des rapports fréquentiels dans les échelles musicales est en grande partie dicté par notre perception naturelle des mélodies, à l'opposé de l'hypothèse selon laquelle la perception des mélodies est modelée culturellement par des échelles musicales qui en sont ainsi un déterminant plutôt qu'une conséquence.
 

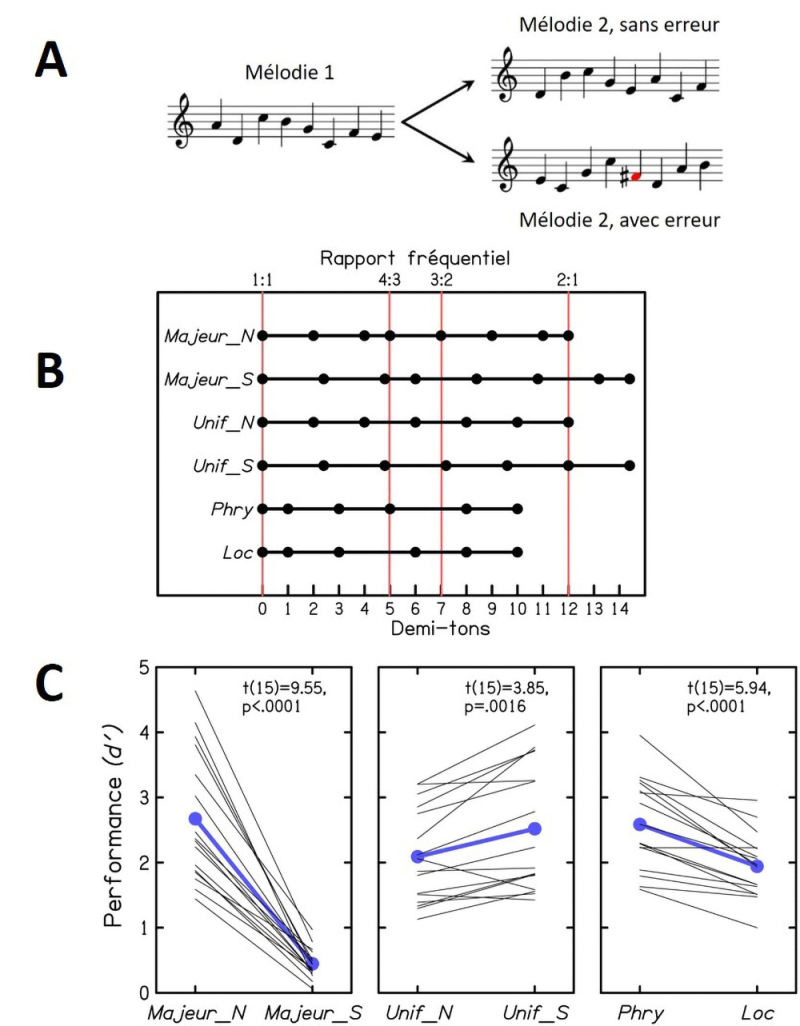
Figure : A. Illustration de la tâche expérimentale. A chaque "essai", deux mélodies étaient présentées. La mélodie 1 était formée de toutes les notes d'une certaine échelle musicale, ordonnées au hasard, en choisissant aussi au hasard le registre fréquentiel de la mélodie ; dans l'exemple dépeint, l'échelle est "Majeur_N", l'échelle diatonique majeure normale. La mélodie 2 réordonnait au hasard les sons de la mélodie 1, soit sans aucune erreur soit avec une erreur d'un demi-ton violant l'échelle de la mélodie 1. Le sujet devait indiquer si la mélodie 2 contenait ou non un son absent de la mélodie 1.  B. Six échelles utilisées dans l'étude. Majeur_S s'obtient en étirant Majeur_N de 20 % ; cet étirement élimine les rapports fréquentiels simples 2:1 et 3:2, présents (presque exactement) dans Majeur_N. Unif_N, échelle chère à Debussy, divise l'octave (2:1) en six intervalles égaux et ne contient pas de rapport fréquentiel simple autre que 2:1. Unif_S étire Unif_N de 20 % ; cet étirement préserve le rapport 2:1, et produit aussi des rapports proches de 3:2 et 4:3. Phry et Loc dérivent des échelles diatoniques dites "Phrygienne" et "Locrienne" ; elles ne diffèrent l'une de l'autre que par leur quatrième degré, formant un rapport simple (4:3) avec le premier degré seulement dans le cas de Phry. C. Performances "finales" obtenues pour les six échelles dépeintes en B. Chaque ligne fine représente un sujet ; en bleu les résultats moyens. On voit dans le panneau gauche que la transformation de Major_N en Major_S a fortement dégradé les performances. Le panneau central montre que la même transformation (un étirement de 20 %) a par contre amélioré les performances de Unif_N à Unif_S. Le panneau de droite indique que les performances ont été meilleures pour Phry que pour Loc. Il ressort de l'ensemble de ces résultats que la performance a été facilitée par la présence de rapports fréquentiels simples (au moins approximativement) dans l'échelle musicale de la mélodie 1.

En savoir plus : Demany L, Semal C, Pressnitzer D. Simple frequency ratios naturally make precisely perceived melodies. Curr Biol. 2025 Mar 6:S0960-9822(25)00193-9. doi: 10.1016/j.cub.2025.02.030. Epub ahead of print. PMID: 40081379.